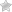Расстояние на плоскости
Учитывая положение X и Y на плоскости, расстояние между двумя точками можно вычислить, используя теорему Пифагора.
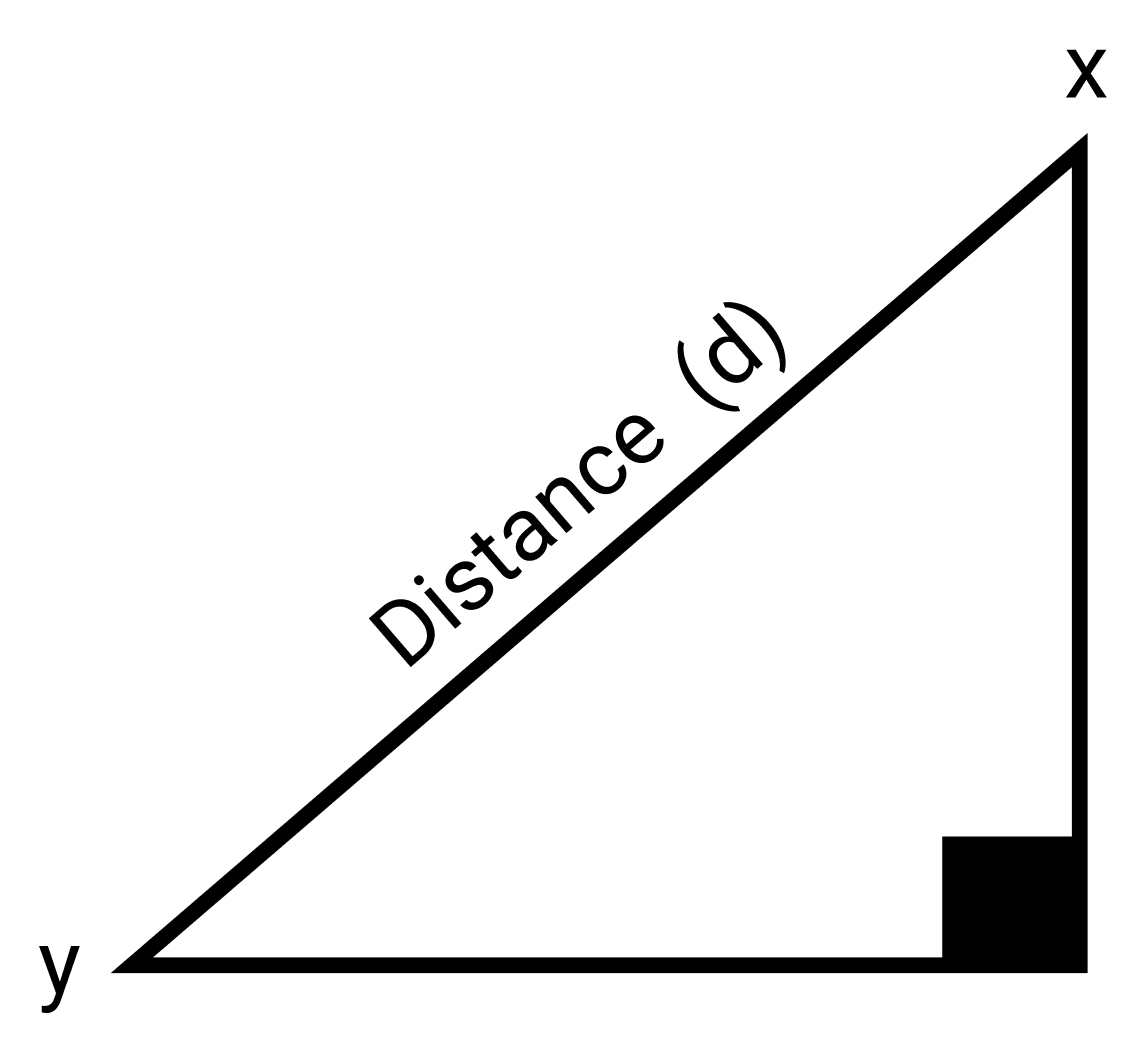
Уравнение для которой выглядит так:
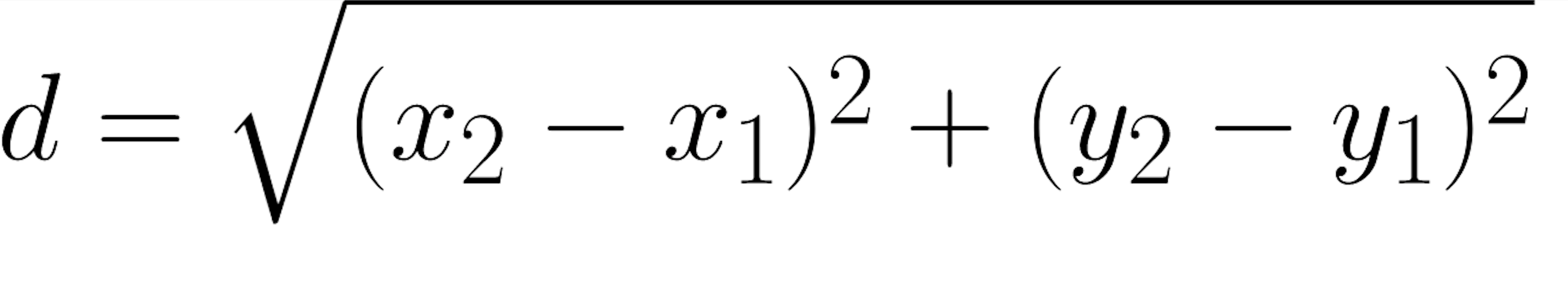
Теперь это можно преобразовать в код:
Во-первых, javascript предоставляет объект Math, который является основной утилитарной библиотекой. Начнём из внутренностей уравнения:
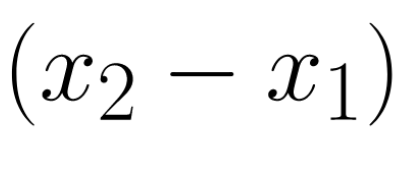
Здесь на самом деле понадобится расчёт абсолютной величины разности, например:
Math.abs(20–5) = 15 или Math.abs(5-20) = 15Затем, результат нужно возвести в квадрат с помощью функции Math.pow():
Math.pow(result, 2);Полученное для x и y надо сложить и получить квадратный корень с помощью Math.sqrt(). Полное уравнение в Javascript будет выглядеть следующим образом:
Math.sqrt(Math.pow(Math.abs(x1 - x2)) + Math.pow(Math.abs(y1 - y2)));Этого будет достаточно для плоскости, но результат будет совершенно неточным при вычислении расстояния для поверхность Земли, которая по сути является сферой (сплюснутый сфероид).
Расстояние на поверхности сферы
Чтобы рассчитать точнее, потребуются два дополнительных уравнения.
Во-первых, понадобится способ вычисления угла между двумя точками от центра сферы, за которым последует уравнение для вычисления расстояния между двумя точками с учетом центрального угла (результат предыдущего уравнения). Используем математические формулы, чтобы реализовать оба. Начнем с вычисления угла между двумя точками от центра.
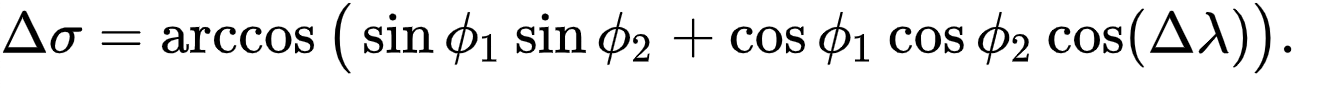
- Δ (delta) представляет разницу
- σ – центральный угол, который надо вычислить
- arcos или обратный косинус (cos в степени -1) в Javascript представлен
Math.acos() - Φ значение широты
- λ значение долготы
Преобразуем это уравнение в код. Но, прежде чем приступим, следует обратить внимание, что придётся иметь дело с радианами, а не с градусами, поскольку это гораздо более точный способ измерения углов, и что более важно, тригонометрия Javascript работает не в градусах, а в радианах.
Для реализации преобразования понадобятся следующие функции:
const degreesToRadians = degrees => degrees * (Math.PI / 180);
const radiansToDegrees = radians => radians * (180 / Math.PI);Затем все, что останется сделать, это поместить оставшуюся часть уравнения в функцию, использующую тригонометрические утилиты Javascript Math. Функция будет выглядеть примерно так:
const centralSubtendedAngle = (locationX, locationY) => {
const locationXLatRadians = degreesToRadians(locationX.latitude);
const locationYLatRadians = degreesToRadians(locationY.latitude);
return radiansToDegrees(
Math.acos(
Math.sin(locationXLatRadians) * Math.sin(locationYLatRadians) +
Math.cos(locationXLatRadians) *
Math.cos(locationYLatRadians) *
Math.cos(
degreesToRadians(
Math.abs(locationX.longitude - locationY.longitude)
)
)
)
);
}Следующее, что нужно будет рассчитать, – это расстояние до дуги centralSubtendedAngle. Это можно описать следующим образом:
2 * PI * {radius of the earth} * ({central subtended angle} / 360);Земля, как полагают, имеет радиус 6371 км. Используем это в Javascript-коде:
const earthRadius = 6371
const greatCircleDistance = angle => 2 * Math.PI * earthRadius * (angle / 360);
const distanceBetweenLocations = (locationX, locationY) =>
greatCircleDistance(centralSubtendedAngle(locationX, locationY));Вызов distanceBetweenLocations выглядит следующим образом:
const NewYork = {latitude: 40.7128, longitude: 74.0060};
const Sydney = {latitude: -33.8688, longitude: -151.2093};
console.log(distanceBetweenLocations(NewYork, Sydney));Последнее замечание: из-за искажений на поверхности Земли этот метод не будет точным на 100%, однако точность будет примерно 0,05% и это достаточно хороший результат.
Calculate the distance between two points on Earth using Javascript